Dissected Squares
Objective: To understand the relationship between area and perimeter in regular polygons.
Materials: For teaching students, hands-on manipulatives are recommended. This
lesson uses our Four Tricky Two Way Puzzles set. This set consists of four
dissected squares of the same size, each of which can be rearranged to form another
regular polygon.
If you have a puzzle, measure the length of the sides of any of the squares, and use this to caluculate the area of the squares.
[The length is 4 inches, so the area is 4x4 = 16 square inches.]
What is the area of the triangle made by rearranging the red square as shown below?
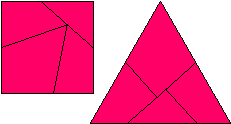
[Since the triangle is made from the same pieces that make up the square, it has
the same area, which is 16 square inches.]
Using this knowledge, calculate the length of an edge of the triangle. Then measure it
with a ruler to see if your answer is correct.
[The area is given by Lsin(60)Lcos(60), from which L can be calculated as 6.08 inches.]
The perimeter of a polygon is the sum of all of the edge lengths. What is the perimeter
of the triangle?
[The perimeter is 3 times the edge length, or 18.24 inches.]
Optional: Calculate the edge length for the pentagon, hexagon, and octagon.
Using a ruler, measure the perimeter of the pentagon, hexagon, and octagon.
[The perimeters are 15.14, 14.80, and 14.56 inches, respectively.]
Compare the perimeter of these five polygons (including the square). What do
you find?
[The greater the number of sides, the less the perimeter. You may want to plot the
perimeter as a function of the number of sides.]
Based on this trend, what shape would you expect would give you the smallest perimeter
for a given area?
[A circle, which can be though of as a regular polygon with an infinite number
of sides.]
What is the perimeter of a circle with area 16 square inches?
[The area is given by (pi)r^2, and the perimeter by 2(pi)r, which allows the perimeter to
be calculated as 2A(square root(pi)) = 14.18 square inches.]
Go to Tessellations Home
Webmaster: Robert Fathauer;
rob@tessellations.com