Regular Polygon Tessellations I

Objective: To understand which regular polygons will tile by themselves, which won't, and why.
Materials: For teaching students, hands-on manipulatives such as Pattern Blocks or Tessel-Gons are recommended.

A polygon is a many-sided shape. A regular polygon is one in which all of the sides and angles are equal. Some examples are shown below.

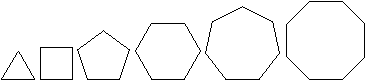
These are referred to as, respectively, (regular) triangle, square, pentagon, hexagon, heptagon, and octagon. A vertex is a point at which three or more tiles in a tessellation meet. Two tiles cannot meet in a point, but would have to meet in line. First, try tessellating with hexagons. This works, as shown below, with three hexagons meeting at each vertex.

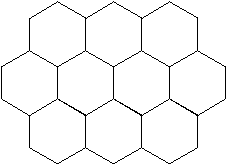
Since the interior angles get larger as the number of sides in a polygon gets larger, no regular polygons with more than six sides can tessellate by themselves. (Hexagons already have the minimum possible number of tiles meeting at each vertex, three.) If you have a Tessel-gons set, you can try tessellating with octagons to illustrate this point. Next, try tessellating with squares. This is also possible, as shown below.

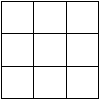
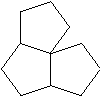
Here four tiles meet at each vertex. Since there are no integers between three and four, pentagons must not tessellate. This is shown below. (Foam rubber regular pentagons can be purchased from Tessellations for $0.25 each, if you want to be able to demonstrate this hands on.)

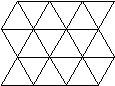
Finally, try tessellating with triangles. This is also possible, as shown below, where the number of tiles meeting at each vertex is six. Since there are no regular polygons with less than three sides, the only regular polygons which will tile be themselves are triangles, squares, and hexagons.

Go to Tessellations Home

Webmaster: Robert Fathauer; rob@tessellations.com