Symmetry in Tessellations
Objective: To understand the different types of mathematical symmetry found in
tessellations.
Materials: For teaching students, hands-on manipulatives are recommended. Any of the
Puzzellations puzzles can be used to illustrate these basic symmetries.
Three types of mathematical symmetry are commonly found in tessellations.
These are translational symmetry, rotational symmetry, and glide reflection symmetry.
Recall when reading this lesson that tessellations extend to infinity; the diagrams
shown below are finite portions of infinite tessellations.
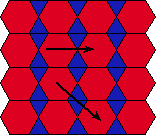
1. Translational Symmetry
A tessellation possesses translational symmetry if it can be translated by some vector
and remain unchanged. Any tessellation with this property has inifinitely many different
translation vectors due to the infinite extent of tessellations. The tessellation below
has translational symmetry; two possible vectors are shown. Find additional vectors.
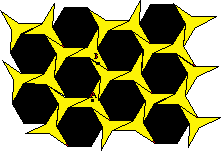
2. Rotational Symmetry
A tessellation possesses rotational symmetry if it can be rotated by some angle about
some point and remain unchanged. A tessellation which can be rotated by 1/n of a full
revolution and remain unchanged is said to posses n-fold rotational symmetry. In the
example below, point A is a point of 3-fold rotational symmetry, while point B is a
point of 2-fold rotational symmetry. Try to identify a point of 6-fold rotational
symmetry.
3. Glide Reflection Symmetry
A tessellation possesses glide reflection symmetry if it can be translated by some
vector and then reflected about that vector and remain unchanged. A special case of glide
rereflection symmetry is simple reflection or mirror symmetry, where the vector has
a value of zero. The example below illustrates glide reflection. Try to find some
lines of simple reflection symmetry for the first tessellation above. Does the second
tessellation above posses glide reflection symmetry?

Using any of the Puzzellations puzzles, pattern blocks, etc., try to construct other
tessellations which exhibit the symmetries discussed here.
Go to Tessellations Home
Webmaster: Robert Fathauer;
rob@tessellations.com