Tetrominoes
Objective: To understand what polyominoes are and to learn how tetrominoes can be
related to tessellations.
Materials: For teaching students, hands-on manipulatives are recommended; in this
case our TetraMania set of tetrominoes are the only commercial set I know of.
A polyomino is a polygon made up of squares joined edge-to-edge. There is only one
type of domino (two squares) and two types of trominoes (3 squares), but there are five
different tetrominoes, as shown here. These can be referred to as the Square, Bar, T,
L, and Skew tetrominoes. Note that the L and Skew tetrominoes are not invariant under
reflection; i.e., the mirror image is not the same as the original.

A great variety of tessellations can be formed from tetrominoes. As one example, try
making a square using four tetrominoes. There are many different ways to do this, and
each of these squares can of course be used as a building block for forming an infinite
tessellation, as squares tessellate.
Now try making a rectangle using one tetromino of each type. You'll find it can't be done.
This can be proven by thinking of the rectangle as a checkerboard, where each square is
one of the four squares making up a tetromino. The Square, Bar, L, and Skew tetrominoes
each take up two shaded and two unshaded squares. However, the T tetromino takes up
three shaded and one unshaded (or one shaded and three unshaded). Since any rectangle
has the same number of shaded and unshaded squares, it is impossible to form any rectangle
containing an odd number of T tetrominoes.

Next experiment with tessellations formed using only L tetrominoes. A couple of examples
are shown here. Try to find some other ones.
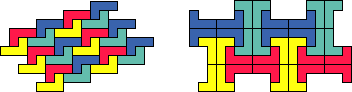
The "basic tessellating set" of tetrominoes is a group of each of the five tetrominoes
which, when copied and translated repeatedly, will cover the mathematical plane. This
group is shown below.
The "reflective tessellating set" of tetrominoes is a group of each of the five tetrominoes
plus the mirror image of the L and Skew tetrominoes (7 total) which, when copied and
translated repeatedly, will cover the mathematical plane. Try to find this group.
The above serves as an introduction to tessellating with tetrominoes. Keep exploring
on your own. Try making different tessellations illustrating the types of symmetry
discussed in the preceding lesson.
Go to Tessellations Home
Webmaster: Robert Fathauer;
rob@tessellations.com